Execute this notebook:
Download locally
Node representation learning with Deep Graph Infomax¶
This demo demonstrates how to perform unsupervised training of several models using the Deep Graph Infomax algorithm (https://arxiv.org/pdf/1809.10341.pdf) on the CORA dataset:
GCN (both as a full-batch method, and with the Cluster-GCN training procedure)
GAT (only as a full-batch method, but the Cluster-GCN training procedure is also supported)
APPNP (as with GAT, only as a full-batch method, but the Cluster-GCN training procedure is also supported)
RGCN
GraphSAGE
HinSAGE
As with all StellarGraph workflows: first we load the dataset, next we create our data generators, and then we train our model. We then take the embeddings created through unsupervised training and predict the node classes using logistic regression.
See the GCN + Deep Graph Infomax fine-tuning demo for semi-supervised training using Deep Graph Infomax, by fine-tuning the base model for node classification using labelled data.
[3]:
from stellargraph.mapper import (
CorruptedGenerator,
FullBatchNodeGenerator,
GraphSAGENodeGenerator,
HinSAGENodeGenerator,
ClusterNodeGenerator,
)
from stellargraph import StellarGraph
from stellargraph.layer import GCN, DeepGraphInfomax, GraphSAGE, GAT, APPNP, HinSAGE
from stellargraph import datasets
from stellargraph.utils import plot_history
import pandas as pd
from matplotlib import pyplot as plt
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.manifold import TSNE
from IPython.display import display, HTML
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.callbacks import EarlyStopping
import tensorflow as tf
from tensorflow.keras import Model
(See the “Loading from Pandas” demo for details on how data can be loaded.)
[4]:
dataset = datasets.Cora()
display(HTML(dataset.description))
G, node_subjects = dataset.load()
Data Generators¶
Now we create the data generators using CorruptedGenerator (docs). CorruptedGenerator returns shuffled node features along with the regular node features and we train our model to discriminate between the two.
Note that:
We typically pass all nodes to
corrupted_generator.flowbecause this is an unsupervised taskWe don’t pass
targetstocorrupted_generator.flowbecause these are binary labels (true nodes, false nodes) that are created byCorruptedGenerator
[5]:
fullbatch_generator = FullBatchNodeGenerator(G, sparse=False)
gcn_model = GCN(layer_sizes=[128], activations=["relu"], generator=fullbatch_generator)
corrupted_generator = CorruptedGenerator(fullbatch_generator)
gen = corrupted_generator.flow(G.nodes())
Using GCN (local pooling) filters...
GCN Model Creation and Training¶
We create and train our DeepGraphInfomax model (docs). Note that the loss used here must always be tf.nn.sigmoid_cross_entropy_with_logits.
[6]:
infomax = DeepGraphInfomax(gcn_model, corrupted_generator)
x_in, x_out = infomax.in_out_tensors()
model = Model(inputs=x_in, outputs=x_out)
model.compile(loss=tf.nn.sigmoid_cross_entropy_with_logits, optimizer=Adam(lr=1e-3))
[7]:
epochs = 100
[8]:
es = EarlyStopping(monitor="loss", min_delta=0, patience=20)
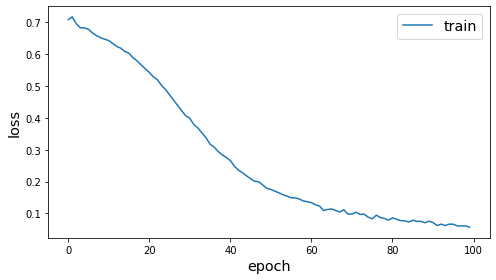
history = model.fit(gen, epochs=epochs, verbose=0, callbacks=[es])
plot_history(history)
Extracting Embeddings and Logistic Regression¶
Since we’ve already trained the weights of our base model - GCN in this example - we can simply use base_model.in_out_tensors to obtain the trained node embedding model. Then we use logistic regression on the node embeddings to predict which class the node belongs to.
Note that the results here differ from the paper due to different train/test/val splits.
[9]:
x_emb_in, x_emb_out = gcn_model.in_out_tensors()
# for full batch models, squeeze out the batch dim (which is 1)
x_out = tf.squeeze(x_emb_out, axis=0)
emb_model = Model(inputs=x_emb_in, outputs=x_out)
[10]:
train_subjects, test_subjects = model_selection.train_test_split(
node_subjects, train_size=0.1, test_size=None, stratify=node_subjects
)
test_gen = fullbatch_generator.flow(test_subjects.index)
train_gen = fullbatch_generator.flow(train_subjects.index)
test_embeddings = emb_model.predict(test_gen)
train_embeddings = emb_model.predict(train_gen)
lr = LogisticRegression(multi_class="auto", solver="lbfgs")
lr.fit(train_embeddings, train_subjects)
y_pred = lr.predict(test_embeddings)
gcn_acc = (y_pred == test_subjects).mean()
print(f"Test classification accuracy: {gcn_acc}")
Test classification accuracy: 0.8002461033634126
This accuracy is close to that for training a supervised GCN model end-to-end, suggesting that Deep Graph Infomax is an effective method for unsupervised training.
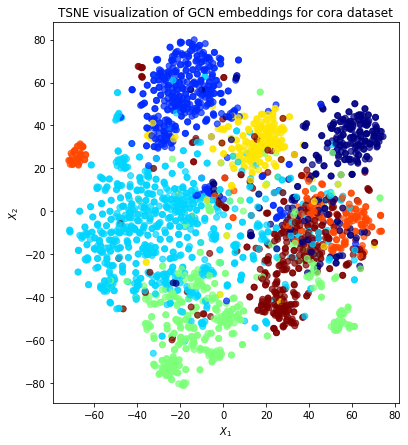
Visualisation with TSNE¶
Here we visualize the node embeddings with TSNE. As you can see below, the Deep Graph Infomax model produces well separated embeddings using unsupervised training.
[11]:
all_embeddings = emb_model.predict(fullbatch_generator.flow(G.nodes()))
y = node_subjects.astype("category")
trans = TSNE(n_components=2)
emb_transformed = pd.DataFrame(trans.fit_transform(all_embeddings), index=G.nodes())
emb_transformed["label"] = y
[12]:
alpha = 0.7
fig, ax = plt.subplots(figsize=(7, 7))
ax.scatter(
emb_transformed[0],
emb_transformed[1],
c=emb_transformed["label"].cat.codes,
cmap="jet",
alpha=alpha,
)
ax.set(aspect="equal", xlabel="$X_1$", ylabel="$X_2$")
plt.title("TSNE visualization of GCN embeddings for cora dataset")
plt.show()
Comparing Different Models¶
Now we run Deep Graph Infomax training for other models. Note that switching between StellarGraph models only requires a few code changes.
[13]:
def run_deep_graph_infomax(
base_model, generator, epochs, reorder=lambda sequence, subjects: subjects
):
corrupted_generator = CorruptedGenerator(generator)
gen = corrupted_generator.flow(G.nodes())
infomax = DeepGraphInfomax(base_model, corrupted_generator)
x_in, x_out = infomax.in_out_tensors()
model = Model(inputs=x_in, outputs=x_out)
model.compile(loss=tf.nn.sigmoid_cross_entropy_with_logits, optimizer=Adam(lr=1e-3))
history = model.fit(gen, epochs=epochs, verbose=0, callbacks=[es])
x_emb_in, x_emb_out = base_model.in_out_tensors()
# for full batch models, squeeze out the batch dim (which is 1)
if generator.num_batch_dims() == 2:
x_emb_out = tf.squeeze(x_emb_out, axis=0)
emb_model = Model(inputs=x_emb_in, outputs=x_emb_out)
test_gen = generator.flow(test_subjects.index)
train_gen = generator.flow(train_subjects.index)
test_embeddings = emb_model.predict(test_gen)
train_embeddings = emb_model.predict(train_gen)
# some generators yield predictions in a different order to the .flow argument,
# so we need to get everything lined up correctly
ordered_test_subjects = reorder(test_gen, test_subjects)
ordered_train_subjects = reorder(train_gen, train_subjects)
lr = LogisticRegression(multi_class="auto", solver="lbfgs")
lr.fit(train_embeddings, ordered_train_subjects)
y_pred = lr.predict(test_embeddings)
acc = (y_pred == ordered_test_subjects).mean()
return acc
Cluster-GCN¶
Cluster-GCN is a scalable training procedure for that works for several “full batch” models in StellarGraph, including GCN, GAT and APPNP. This example just trains on GCN. The training mechanism breaks the graph into a number of small subgraph “clusters” and trains a single GCN model on these, successively. It is equivalent to full-batch GCN with a single cluster (clusters=1), but with
clusters > 1 random clusters (as used here), its performance will be less than GCN. With better clusters, Cluster-GCN performance should be much improved.
(Note: ClusterNodeGenerator can be used with Neo4j for scalable training on large graphs, including unsupervised via Deep Graph Infomax.)
[14]:
cluster_generator = ClusterNodeGenerator(G, clusters=12, q=4)
cluster_gcn_model = GCN(
layer_sizes=[128], activations=["relu"], generator=cluster_generator
)
def cluster_reorder(sequence, subjects):
# shuffle the subjects into the same order as the sequence yield
return subjects[sequence.node_order]
cluster_gcn_acc = run_deep_graph_infomax(
cluster_gcn_model, cluster_generator, epochs=epochs, reorder=cluster_reorder
)
print(f"Test classification accuracy: {cluster_gcn_acc}")
Number of clusters 12
0 cluster has size 225
1 cluster has size 225
2 cluster has size 225
3 cluster has size 225
4 cluster has size 225
5 cluster has size 225
6 cluster has size 225
7 cluster has size 225
8 cluster has size 225
9 cluster has size 225
10 cluster has size 225
11 cluster has size 233
Test classification accuracy: 0.6308449548810501
GAT¶
GAT is a “full batch” model similar to GCN. It can also be trained using both FullBatchNodeGenerator and ClusterNodeGenerator, including for Deep Graph Infomax.
[15]:
gat_model = GAT(
layer_sizes=[128], activations=["relu"], generator=fullbatch_generator, attn_heads=8,
)
gat_acc = run_deep_graph_infomax(gat_model, fullbatch_generator, epochs=epochs)
gat_acc
print(f"Test classification accuracy: {gat_acc}")
Test classification accuracy: 0.4716981132075472
APPNP¶
APPNP is a “full batch” model similar to GCN. It can also be trained using both FullBatchNodeGenerator and ClusterNodeGenerator, including for Deep Graph Infomax.
[16]:
appnp_model = APPNP(
layer_sizes=[128], activations=["relu"], generator=fullbatch_generator
)
appnp_acc = run_deep_graph_infomax(appnp_model, fullbatch_generator, epochs=epochs)
print(f"Test classification accuracy: {appnp_acc}")
Test classification accuracy: 0.440935192780968
GraphSAGE¶
GraphSAGE is a sampling model, different to the models above.
[17]:
graphsage_generator = GraphSAGENodeGenerator(G, batch_size=1000, num_samples=[5])
graphsage_model = GraphSAGE(
layer_sizes=[128], activations=["relu"], generator=graphsage_generator
)
graphsage_acc = run_deep_graph_infomax(
graphsage_model, graphsage_generator, epochs=epochs
)
print(f"Test classification accuracy: {graphsage_acc}")
Test classification accuracy: 0.7210828547990156
Heterogeneous models¶
Cora is a homogeneous graph, with only one type of node (paper) and one type of edge (type). Models designed for heterogeneous graphs (with more than one of either) can also be applied to homogeneous graphs, but it is not using their additional flexibility.
HinSAGE¶
HinSAGE is a generalisation of GraphSAGE to heterogeneous graphs that can be trained with Deep Graph Infomax. For homogeneous graphs, it is equivalent to GraphSAGE and it indeed gives similar results.
[18]:
hinsage_generator = HinSAGENodeGenerator(
G, batch_size=1000, num_samples=[5], head_node_type="paper"
)
hinsage_model = HinSAGE(
layer_sizes=[128], activations=["relu"], generator=hinsage_generator
)
hinsage_acc = run_deep_graph_infomax(hinsage_model, hinsage_generator, epochs=epochs)
print(f"Test classification accuracy: {hinsage_acc}")
Test classification accuracy: 0.7042657916324856
RGCN¶
RGCN is a generalisation of GCN to heterogeneous graphs (with multiple edge types) that can be trained with Deep Graph Infomax. For homogeneous graphs, it is similar to GCN. It normalises the graph’s adjacency matrix in a different manner and so won’t exactly match it.
[19]:
from stellargraph.mapper import RelationalFullBatchNodeGenerator
from stellargraph.layer import RGCN
rgcn_generator = RelationalFullBatchNodeGenerator(G)
rgcn_model = RGCN(layer_sizes=[128], activations=["relu"], generator=rgcn_generator)
rgcn_acc = run_deep_graph_infomax(rgcn_model, rgcn_generator, epochs=epochs)
print(f"Test classification accuracy: {rgcn_acc}")
Test classification accuracy: 0.7366694011484823
Overall results¶
The cell below shows the accuracy of each model.
[20]:
pd.DataFrame(
[gat_acc, gcn_acc, cluster_gcn_acc, appnp_acc, graphsage_acc, hinsage_acc, rgcn_acc],
index=["GAT", "GCN", "Cluster-GCN", "APPNP", "GraphSAGE", "HinSAGE", "RGCN"],
columns=["Accuracy"],
)
[20]:
| Accuracy | |
|---|---|
| GAT | 0.471698 |
| GCN | 0.800246 |
| Cluster-GCN | 0.630845 |
| APPNP | 0.440935 |
| GraphSAGE | 0.721083 |
| HinSAGE | 0.704266 |
| RGCN | 0.736669 |
Conclusion¶
This notebook demonstrated how to use the Deep Graph Infomax algorithm to train other algorithms to yield useful embedding vectors for nodes, without supervision. To validate the quality of these vectors, it used logistic regression to perform a supervised node classification task.
See the GCN + Deep Graph Infomax fine-tuning demo for semi-supervised training using Deep Graph Infomax, by fine-tuning the base model for node classification using labelled data.
Execute this notebook:
Download locally
